過程 |
|
指導上の留意点(○)、評価規準と評価方法(◇)
算数的活動(◎) |
|
つかむ |
1 |
本時の問題を知り、課題をとらえる。
(数学的な思考力・判断力・表現力を育む学習プリント」(佐賀県教育センター)を使用する。) |
|
|
しんいちさんは、次の問題について考えています。
[問題]
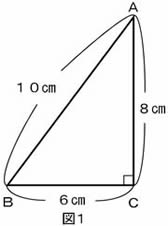
右の図1のような直角三角形があります。
この三角形に1本の直線を引いて、2つの三角形に分けます。そのとき、分けられた三角形の面積の比は1:2になるようにします。
どんな直線を引いたらよいでしょうか。
|
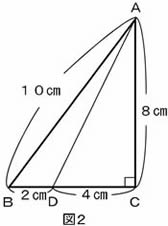
そこで、しんいちさんは図2のように直線を引き、次のように説明しました。
[説明]
まず、辺BCを2cmと4cmに分ける点Dをとります。
次に頂点Aから点Dに向かって直線を引きます。
すると、三角形ABDと三角形ACDの面積の比は、1:2になります。 |
しんいちさんの説明が正しい理由を、図、式、言葉を使って説明しましょう。 |
 |
 |
|
比の考えを使って、三角形の面積の比が1:2になる理由を考えよう |
|
|
|
|
見通す |
2 |
解決の見通しをもつ。 |
| |
・ |
辺BCを1:2の比に分割する辺BC上点Dをとり点Aから直線を引く。 |
| |
・ |
三角形ABDと三角形ACDの面積を求め、それらの比が1:2になっているかを調べる。 |
|
| ○ |
三角形の面積というキーワードに注目させ、面積を求める公式を想起させる。
|
| ○ |
点Dは、辺BCを1:2か2:1に分ける点であり、どちらになってもよい。 |
|
| 自力解決 |
3 |
自力解決をする。 |
| |
《予想される児童の考え》 |
| |
① |
底辺の長さに対して比の考えを使う。
三角形ABDと三角形ACDの高さは等しい。
よって、
辺BD:辺CD=1:2となる点Dを見つければよい。
辺BC全体は、1+2(=3)にあたるので、
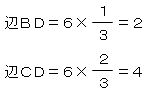 となる。 となる。
辺BDは2cm、辺CDは4cmとなるので、
しんいちさんの直線の引き方でよい。
|
| |
② |
面積に対して比の考えを使う。
三角形ABDの面積=2×8÷2=8 8c㎡
三角形ACDの面積=4×8÷2=16 16c㎡
だから、2つの三角形の面積の比は、
三角形ABDの面積:三角形ACDの面積
=8:16=1:2 となる。
だから、しんいちさんの直線の引き方でよい。 |
|
| ◎ |
1つの方法で求めたら、他の方法も考えさせる。(ア)
|
| ◎ |
この後の学び合いの活動で友達に説明させるために、ノートに図、式、言葉などを用いて記述するようにさせる。(ア) |
| ○ |
①は辺BCの割合を求めて考え、②は2つの三角形の面積の比から考える方法である。
①は、全体の割合を求める考えであり、本単元の基本問題の学習プリント(佐賀県教育センター)の大問4を振り返ることで、確認できる。
②は、「辺BCを2cmと4cmに分ける」という表現を基にした考えであり、比較的児童が考えやすい方法である。 |
|
| 学び合い |
|
| ◎ |
自分の考えを説明する際には、ノートを示しながら説明させる。(イ) |
| ◎ |
自分の考えを説明させる際には、児童が発言する次のような言葉に注目し、児童の考えをつなげていく。 (イ) |
| |
・まず…自分の考えを分割し、整理しようする言葉。
・でも…反例をあげ、考えを説明しようとする言葉。
・だったら…友達の考えを基にして、その先を考えて
説明しようとする言葉。
・もし…条件を変えたり、考えを整理したり、一般化
を図ったりしようとする言葉。 |
| ◎ |
これまでの学習を基に、言葉や図、式などを関連付けて説明させる。(イ) |
| ◎ |
自分のやり方と同じか違うかを意識させながら聞かせる。また、よく分からないところは、お互いに質問し合わせる。(イ) |
| ◎ |
説明を聞いて、自分の考えと異なる考えやよい考えがあったらノートにかかせる。(イ) |
◇ 比の考えを使って、三角形の面積の比が1:2になる理由を筋道を立てて考えている。
【数学的な考え方】[ノート、行動観察] |
|
5 |
考えたことをグループの代表が発表・板書し、全体で話し合う。
|
|
| ◎ |
①と②を、全体の比を求めている点で関連付け、既習の考えを活用するよさに気付かせる。(イ) |
|
| ≪児童が実際にノートにかいた考え≫ |
 |
「2つの三角形の面積を求めて考えたノート例」
※上記の「面積を分数であらわします」という表現は、2つの三角形の面積の比の値を求めていると考えられる。
|
|
| |
| ○ |
上記の≪児童が実際にノートにかいた考え≫のように辺BDが2cm、辺CDが4cmであることを用いて説明を行った場合も、根拠を明らかにして筋道を立てて表現できていれば良いこととする。 |
|
| まとめる |
6 |
本時の学習で学んだことを算数日記に書く。 |
| ≪児童が実際に書いた算数日記の例≫ |
 |
| ※上の算数日記は、友達の考えのよさに気付き、自分の考えとして取り入れる態度が育っている例である。 |
|
| ○ |
友達の考えを読み取ろうとした姿を称賛し、友達が表現した式や言葉、図などから読み取る力も大切であることを確認する。 |
| ○ |
授業で分かったことや感想、これから気を付けたいことやさらに調べてみたいことなどを書かせるようにする。 |
| |
|
|