�ߒ� |
|
�w����̗��ӓ_�i���j�A�]���K���ƕ]�����@�i���j
�Z���I�����i���j |
|
���� |
| �� |
�@�R���̃O���[�v��Ґ�����B
|
�P |
�@�{���̖���m��A�ۑ���Ƃ炦��B |
|
�� |
�O���[�v�S���������������A��̓I�Ɋ����ł���悤��{�I�ɂP�̃O���[�v���R���ŕҐ����邱�Ƃ��]�܂����B |
| �� |
�������c�����}�W�b�N�A�d��A�Pm��K�i�e�O���[�v�j |
|
�k���l�@�u�R���̗p���̌`�́A�������ȁH�v�@ 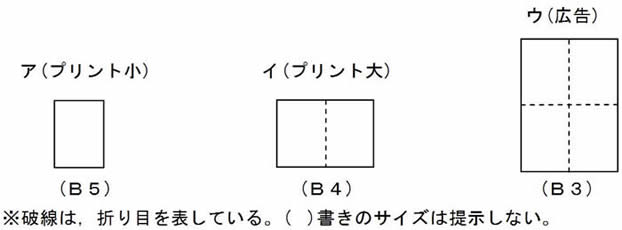
|
|
| |
��\�z����鎙���̔����� |
| |
�E |
�u�����`�̒����`�݂�������B�v |
| |
�E |
�u���̑傫�����Ⴄ�̂ɁA�Ȃ��A���ꂢ�ɐ܂肽���߂Ă���̂��낤�B�v |
| |
�E |
�u�����ɐ܂�����A�d�Ȃ�̂����肻������B�v |
| |
�E |
�u�C�̌�����ς��Ă݂���A�ǂ�������`�݂����B�v |
|
| �� |
�����̐g�߂ɂ�����̂̒������ނ�I�Ԃ��ƂŁA���C�Ȃ����Ă����p���̌`�ɁA�������܂肪���肻���Ȃ��ƂɋC�t������B�܂��A�Î��̃��T�C�N���̍ۂɂ悭�ڂɂ���A�V������L���Ȃǂ𑩂˂Ď��R�ł��ꂢ�ɂЂƂ�����ɂ������̂���A�����̒�����A�L���A�v�����g���L���č��Ɍf������B���̂悤�Ȋ�����ʂ��āA�Z���Ŋw���Ƃ���퐶���̒��Ɍ��o�����Ƃ���ԓx�̈琬���˂炤�B |
| �� |
�O���[�v���ɃA�`�E�̗p�����P�����z�z���A�C�t���\������B |
|
�ӂ̒����ɖڂ�t���āA�����`���ǂ����ׂ悤 |
|
���ʂ� |
�Q |
�@�����̌��ʂ������B |
| |
�@ |
�A�̗p�����C��E�ɕ~���l�߁A��������̐��������藧���ׂ�B |
| |
�A |
�P�����c�Ɖ��̒����𑪂�A��̒l�Œ��ׂ�B |
| |
�B |
�p�����d�˂��Ƃ��̊e�����`�̒��_�̕��ѕ��̋K��������ɁA�ސ�����B |
|
| �� |
�u�`�������ł���v���Ƃɂ��āA���ʗ���������B
�u�p���̌`�́A�S�Ē����`�ł���A�c�Ɖ��ɓ����悤�Ɉ����̂�����A�k�߂��肵�ďd�˂�A�҂�����Əd�Ȃ�ƍl������B�܂�A�Q�̗p���̏c�̒����Ɖ��̒����̔䂪��������A�Q�̗p���̌`�������ł���Ƃ����Ă悢�v�Ƃ������Ƃ����ʗ��������邽�߂ɁA���𑪒肵�A��������Γ����`�Ƃ�����̂����l��������B(�)
|
���@�g�߂Ȑ����̒��ŁA�䂪���p����Ă��邩�ǂ�����i��ōl���悤�Ƃ��Ă���B
�y�Z���ւ̊S�E�ӗ~�E�ԓx�z[�m�[�g�A�s���ώ@] |
|
| ���͉��� |
|
| |
|
| |
|
| �� |
�A�̍l���ł́u�A�`�E�͓����`�ł���v�Ƃ́A�����ɂ͂����Ȃ����A�����̔��B�i�K�Ƌ��ނ̓������l�����A�u�����`�ł���v�ƌ��_�t���A�c�Ɖ��̒����̔���A��̒l��p���Ĕ�ׂ邱�Ƃ̗L�p�����m�F����B |
| |
|
| �� |
���̂Q�̐}�̂悤�ɁA�p�����d�˂āA���o�I�ɂƂ炦�A�K�������璲�ׂ����l������B���̍l�����́A�}�`�̊g��Ək��(���K)�̓��e�ł���A���������炩�ł͂Ȃ��B�������A���ւȂ���l���Ƃ��đ�ɂ������B |
���@�����`�������`���ǂ����̔��ʂɁA��������̐������̒l�����p���Ă���B
�y���w�I�ȍl�����z[�m�[�g�A�s���ώ@] |
|
| �w�э��� |
�S |
�@�l�������Ƃ��O���[�v�̑�\�����\�E�����A�S�̂Řb�������B
|
| |
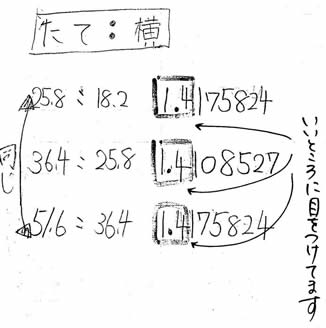
�᎙�������ۂɂ������l���� |
|
�u�A�̔�̒l���g���čl�����m�[�g��v |
| |
�E |
�@�����B�̍l�����������B |
| |
|
�u�A�ƃE�̌`�͓����ł��B�v
�u�ł��A�C�ƃE�������`�݂��������ǁc�v
�u�����A�C���c�ɂ��Ă݂���c�v
�u�����āA��̒l�ׂāA���ꂪ������������Ӕ䂪�������Ƃ�����ˁB�v
�u��̒l�́A�قƂ�Ǔ������ˁB�v
�u���Ⴀ�A�C�ƃE�̌`�́A�������ˁB�v
�u��������A�A�ƃE�̌`�͓����c
�@�@
�����āA�C�ƃE�̌`������������c
�@�@
�A�`�E�̂ǂ���`�������I�v
|
|
| �� |
�����̍l�������������ۂɂ́A�������������鎟�̂悤�Ȍ��t�ɒ��ڂ��A�����̍l�����Ȃ��Ă����B(�)
�E�܂��c�����̍l�������A�������悤���錾�t�B
�E�ł��c����������A�l����������悤�Ƃ��錾�t�B
�E��������c�F�B�̍l������ɂ��āA���̐���l��
�@�@�@�@�@�@�@
�Đ������悤�Ƃ��錾�t�B
�E�����c������ς�����A�l����������A��ʉ�
�@�@�@�@
��}�����肵�悤�Ƃ��錾�t�B
|
| �� |
����܂ł̊w�K����ɁA���t��}�A���Ȃǂ��֘A�t���Đ���������B(�) |
| �� |
�����̂����Ɠ������Ⴄ�����ӎ������Ȃ��畷������B�܂��A�悭������Ȃ��Ƃ���́A���݂��Ɏ��₵���킹��B(�) |
| �� |
�������āA�����̍l���ƈقȂ�l����悢�l������������m�[�g�ɂ�������B(�) |
|
| �܂Ƃ߂� |
�T |
�@�{���̊w�K���Z�����L�ɂ܂Ƃ߂�B |
| �᎙�������ۂɏ������Z�����L�̗�� |
 |
|
| �� |
�����g�����p���́A�a�T�`�a�R�̗p���ł��邱�ƂƁA�֗��Ȕ����퐶���ɐ������Ă��邱�Ƃ�m�点�A��ւ̊S��[�߂�����B |
| �� |
���Ƃŕ����������Ƃ⊴�z�A���ꂩ��C��t���������Ƃ₳��ɒ��ׂĂ݂������ƂȂǂ���������悤�ɂ���B |
|
