過程 |
学 習 活 動 |
指導上の留意点(・)、評価規準と評価方法(◎○)
算数的活動(◇)、ICT利活用(◆) |
つかむ |
[問題]
半径が10㎝の円の面積をもっとくわしく求めてみよう。そして、円の面積の公式を考えてみよう。 |
|
| ◆ |
電子黒板を用いて問題の図を提示し、課題を捉えさせる。 |
・ |
前時までの学習を振り返り、円の面積は半径を1辺とする正方形の面積の約3.1倍だったことを想起させる。 |
|
|
|
| 見通す |
| 2 |
解決の見通しをもつ。 |
| |
《予想される児童の考え》
・平行四辺形に変形させる。
・長方形に変形させる。
|
|
・ |
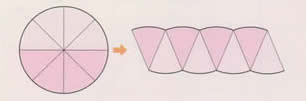
円を8等分して並び替えた図形を提示し、既習の図形に変形させて考えることを確認する。 |
| |
 |
|
| 自力解決 |
| 3 |
自力解決をする。 |
・ |
円を半径で等分して並び替えると、どんな形に変形できるかを考える。 |
| |
|
・ |
円を16等分して並び替えることで、面積の求め方を考える。
|
|
| ◇ |
円を16等分して並び替えることで、既習の図形に変形して面積を求めることができないか考えさせる。 (ア) |
・ |
この後の学び合いにおいて、友達に考えを分かりやすく説明させるために、変形した図形はノートに貼らせ、数や式、言葉などを書き加えさせる。 |
○ 平行四辺形や三角形などの既習の図形に変形して、円の面積を求めようとしている。
【関心・意欲・態度】(観察、ノート)
A 既習の図形に変形して、円の面積を1つの方法で求め、更に他の方法でも求めようとしている。
B 既習の図形に変形して、円の面積を求めようとしている。
〔「努力を要する」状況(C)と判断した児童への指導〕
パソコンを用いて、円から平行四辺形に変形する様子を見せ、操作活動につなげさせる。 |
| ※ |
第1時の円の面積の大きさについて見当を付ける学習で、「努力を要する」状況(C)である児童が「おおむね満足できる」状況(B)となるよう指導する。また、本時において「十分満足できる」状況(A)になった児童がいれば記録に残す。 |
|
| 学び合い |
4 |
自分の考えをグループで説明し合う。 |
・ |
既習の図形と関連付けて円の面積を求め方を考え、説明する。 |
|
| ◇ |
円を16等分した図形を並び替えて面積を求めたことについて、式や言葉を用いて説明させる。(イ) |
・ |
数や式が円のどの部分に当たるのか考えさせる。 |
|
5 |
全体の場で、円の面積の求め方について話し合う。 |
| |
| 《児童がノートに書いた考え》 |
|
| |
|
「電子黒板を用いて三角形の場合について確認している様子」 |
|
◆ |
電子黒板を用いて児童のノートを拡大提示し、円を16等分して並び替えたものを基に説明させる。 |
◆ |
8等分、16等分、32等分、64等分にした円を等積変形した様子をアニメーションで見せることで、だんだんと長方形に近付いていることに気付かせる。 |
| |
   |
| |
  |
| |
|
・ |
長方形とみられる図形の縦の長さ、横の長さは、円のどの部分と同じになるか確認をする。 |
・ |
長方形の縦の長さは円の半径、横の長さは円周の半分(直径×3.14÷2)と同じになることから、円の面積=半径×半径×3.14になることについて考えさせる。 |
・ |
16等分したものを並び替えて、三角形として面積を求めようとした児童がいれば取り上げる。その際、円の分割の仕方によっては、並び替えて三角形に変形できるとは限らないが、既習の図形の面積の求め方を用いて考えていることを評価する。 |
○ 平行四辺形や三角形などの面積の求め方を基に、円の面積の求め方を考えている。
【数学的な考え方】(観察、ノート)
A 円の面積の求め方を図や式や言葉を用いて、2つ以上の方法で説明している。
B 円の面積の求め方を図や式や言葉を用いて、1つの方法で説明している。
〔「努力を要する」状況(C)と判断した児童への指導〕
パソコンを用いて、円から平行四辺形に変形する様子を見せ、底辺や高さに当たる部分がもとの円のどの部分の長さになっているか確認させる。
|
| ※ |
「努力を要する」状況(C)である児童が「おおむね満足できる」状況(B)となるよう指導し、「十分満足できる」状況(A)の児童がいれば記録に残す。 |
|
| まとめる |
| |
円の面積は半径×半径×3.14の計算をすることで求めることができる。 |
8 |
本時の学習を算数日記にまとめる。 |
| |
《児童が実際に書いた算数日記の例》 |
| |
  |
|
・ |
円の面積もこれまでに学習した面積の求め方と関連付けて考えることで公式をつくることができることについてまとめる。 |
・ |
円の面積の公式を用いて、半径10㎝の円の面積を計算させ、前時の方眼を用いて面積を求めたときとほぼ近い値になっていることを確認する。 |
| |
|
・ |
授業で分かったことや感想、これから気を付けたいことや更に調べてみたいことなどを書かせるようにする。 |
|