過程 |
学 習 活 動 |
指導上の留意点(・)、評価規準と評価方法(◎○)
算数的活動(◇)、ICT利活用(◆) |
つかむ |
| 1 |
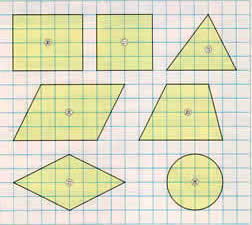
今までの面積の単元の学習を振り返る。 |
・ |
既習の面積の公式について確認する。 |
| |
 |
| |
|
2 |
本時の問題を知り、課題を捉える。 |
|
[問題]
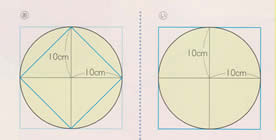
半径10㎝の円の面積について、下の図のように円の内と外に正方形をかいて、見当を付けてみましょう。
 |
|
| ◆ |
円周が直径の何倍かを考えたときのことを想起させるために、電子黒板で既習事項を確認する。 |
| |
|
| |
「既習事項の確認のために用いたスライド」 |
| |
|
・ |
長方形、三角形、平行四辺形などの図形の面積は、それぞれ公式を用いて求められることを振り返らせる。また、円の面積はどのようにして求められるかを問い、関心をもたせる。 |
・ |
円のおよその面積の大きさに着目するようにさせる。 |
|
半径10㎝の円の面積について、見当を付けてみよう。 |
|
| 見通す |
|
・ |
円周の長さを直径の3倍よりも大きく4倍より小さいと見積もったことを想起させ、およその大きさを考えることの意味を捉えさせる。 |
|
| 自力解決 |
| 4 |
自力解決をする。 |
・ |
円に内接する正方形と外接する正方形を利用して、円の面積の見当を付ける。 |
|
| ◇ |
円の面積は、円に内接する正方形と外接する正方形の間にあることから、円のおよその面積について調べさせる。 (ア) |
|
| 学び合い |
5 |
自分の考えをグループや全体で説明し合う。 |
・ |
円の面積は、半径1辺とする正方形の2倍と4倍の間にあることを説明する。 |
| |
《予想される児童の考え》 |
|
・1辺が10㎝の正方形のいくつ分かで考えると、2つ分より大きく、4つ分より小さい。
(10×10)×2=200c㎡
(10×10)×4=400c㎡
だから、半径10㎝の円の面積は、
(10×10)×2より大きく(10×10)×4より小さい。 |
| 《児童がノートにかいた考え》 |
 |
| 「十分満足できる」状況(A)と判断したノート記述の例 |
|
| ◇ |
円のおよその面積について、図や式や言葉などを用いて説明させる。(イ) |
| |
|
| ◆ |
書画カメラを用いて児童のノートを拡大提示し、それを用いて説明させる。 |
| |
|
・ |
面積は200c㎡と400c㎡の間にあることから、およそ300c㎡程であることを確認する。 |
◎ 正方形を用いて、円のおよその面積について見当を付けようとしている。
【関心・意欲・態度】(観察、ノート)
A 円の面積について、円に内接する正方形と外接する正方形を基に見当を付けようとしている。
B 円の面積について、円に内接する正方形または外接する正方形を基に見当を付けようとしている。
〔「努力を要する」状況(C)と判断した児童への指導〕
半径を1辺とする正方形の4つ分の面積をパソコンで示し、円の面積と比べさせて見当を付けさせる。 |
| ※ |
学習活動の観察や授業後のノート記述の分析を基に、全員を対象とした評価を行い記録に残す。 |
|
| まとめる |
6 |
本時の学習をまとめる。 |
| |
円の面積は、半径を1辺とする正方形の面積の2倍より大きく、4倍より小さい。 |
7 |
本時の学習を算数日記にまとめる。 |
| |
《児童が実際に書いた算数日記の例》 |
| |
  |
|
・ |
円のおよその面積について、円に内接する正方形と外接する正方形の間にあると見当を付けたことについてまとめる。 |
| |
|
・ |
授業で分かったことや感想、これから気を付けたいことや更に調べてみたいことなどを書かせるようにする。 |
|