�ߒ� |
�w�@�K�@���@�� |
�w����̗��ӓ_�i�E�j�A�]���K���ƕ]�����@�i�����j
�Z���I�����i���j�A�h�b�s�����p�i���j |
���� |
|
�E |
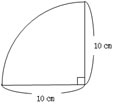
�~�̖ʐς�~�̔����̌`�̖ʐς̋��ߕ��ɂ��āA�f��������p���ĐU��Ԃ点��B |
|
| �Q |
�{���̖���m��A�ۑ�𑨂���B |
| |
|
| |
�u�d�q����p�������̗l�q�v |
|
�� |
�d�q���Ŗ��̐}����A�}�̒��ɂǂ̂悤�Ȍ`�����t���邱�Ƃ��ł��邩���l��������B
�kPowerPoint�����l |
| |
|
�E |
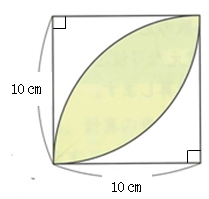
���̐}�̖ʐς����߂��R�̎��i�`����A�a����A�b����j����A�{���͑��҂̍l��������ǂݎ��w�K�ł��邱�Ƃ�`����B |
|
[���]
�`����A�a����A�b���A���̐}�̐F��t���������̖ʐς̋��ߕ����Љ�܂����B�ǂ̂悤�ȋ��ߕ��������̂��A����ǂݎ��A�}�⌾�t���g���Đ������܂��傤�B |
�} |
 |
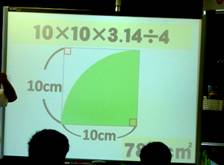
�kA����l
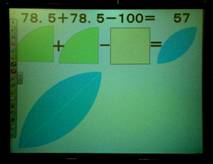
�@78.5�|50��28.5
�@28.5�~�Q��57
�@�@�@�@�����@57c�u |
�k�a����l
�@100�|78.5��21.5
�@21.5�~�Q��43
�@100�|43��57
�@�@�@�@�@�����@57c�u |
�kC����l
�@78.5�{78.5�|100��57
�@�@�@�@�@�@�@�@�@�@�@�����@57c�u |
|
|
����ǂݎ��A�ʐς̋��ߕ���������悤�B |
|
| ���ʂ� |
| �R |
�����̌��ʂ������B |
�E |
����100�A78.5�A50�̐��l�͂ǂ��̕����̖ʐς�\���Ă���̂����l����B |
 |
|
| |
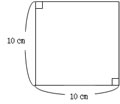
�@�@�@�u�����`�v |
�u 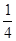 �̉~ �̉~�v |
| |
 |
| |
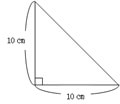
�@�@�u���p�ӎO�p�`�v |
|
�E |
���K�̖ʐς̌�����p���邱�ƂŁA�����ɋ��߂�ꂻ���ȕ����ɂ��čl�������A 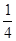 �̉~���B��Ă��邱�ƂɋC�t������B �̉~���B��Ă��邱�ƂɋC�t������B |
�E |
100�͐����`�̖ʐρA78.5�͔��a10�p�̉~��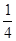 �̖ʐρA50�͒��p�ɂȂ�Q�̕ӂ̒�����10�p�̒��p�ӎO�p�`�̖ʐςł��邱�Ƃɂ��āA���K�̖ʐς̌�����p���Čv�Z�����Ċm�F����B �̖ʐρA50�͒��p�ɂȂ�Q�̕ӂ̒�����10�p�̒��p�ӎO�p�`�̖ʐςł��邱�Ƃɂ��āA���K�̖ʐς̌�����p���Čv�Z�����Ċm�F����B |
| |
|
| |
�u���K�����̊m�F�̂��߂ɗp�����X���C�h�v |
|
| ���͉��� |
| �S |
���͉���������B |
�E |
�`����A�a����A�b�����̖ʐς����߂�����ǂݎ��A�}�⎮�⌾�t��p���ĕ\���B |
| |
|
| |
�s�\�z����鎙���̍l���t |
�E |
�`����̎��ɂ��āA�}�������A���Ɗ֘A�t���čl����B |
| |
 |
| |
|
�E |
�a����̎��ɂ��āA�}�������A���Ɗ֘A�t���čl����B |
| |
 |
�E |
C����̎��ɂ��āA�}�������A���Ɗ֘A�t���čl����B |
| |
 |
| |
|
| |
|
| |
�u�h�b�s��p���ăq���g�������Ă���l�q�v |
|
| �� |
���K�̖ʐς̌����i�~��O�p�`�Ȃǁj��p���āA���G�Ȑ}�`�̖ʐς̋��ߕ��ɂ��čl��������B�i�A�j |
| |
|
| |
|
| |
|
�E |
�`�A�a�A�b�̂R�l�̒��ŁA���������g�݂₷���l�����玮��ǂݎ�点��B�܂��A���̌�̊w�э����ɂ����āA�F�B�ɍl������₷�����������邽�߂ɁA�m�[�g�ɐ}�⎮�⌾�t��p���ċL�q������B |
| |
|
| |
|
���@�ʐς����߂�������l������ǂݎ��A�}�Ǝ������ѕt���Đ������Ă���B
�@�@�@�@�@�@�@�@�@�@�@�@
�y���w�I�ȍl�����z�i�ώ@�A�m�[�g�j
�`�@�Q�ȏ�̍l�����̎���ǂݎ��A�}�⎮�⌾�t��p���Ėʐς̋��ߕ��ɂ��ċL�q���Ă���B
�a�@�P�̍l�����̎���ǂݎ��A�}�⎮�⌾�t��p���Ėʐς̋��ߕ��ɂ��ċL�q���Ă���B
�k�u�w�͂�v����v��(�b)�Ɣ��f���������ւ̎w���l
�@
�`����̎��ɂ��āA�q���g�ɂȂ�悤�ȃA�j���[�V�����������A�}�Ǝ����֘A�t��������B
�kPowerPoint�����F�`����̎��l |
| �� |
�w�K�����̊ώ@����ƌ�̃m�[�g�L�q�̕��͂���ɁA�S����ΏۂƂ����]�����s���L�^�Ɏc���B |
|
| �w�э��� |
�T |
�����̍l�����O���[�v�Ő����������B |
�E |
�}�⎮�⌾�t���֘A�t���āA�l�������Ƃ��݂��ɓ`�������B |
| |
|
| |
�u�F�B�Ɛ����������l�q�v |
|
| �� |
�}�Ǝ���Ή������Ȃ�������������A����_��ގ��_�����t��������B�i�C�j |
| |
|
| �� |
�F�B�ƍl�����𗬂��đ��ݕ]������������A�����ɂȂ��l���̓m�[�g�Ƀ������������肷��B�i�C�j |
| |
|
|
�U |
�S�̂̏�ŁA���ꂼ��̍l�����ɂ��Ęb�������B |
| |
|
| |
|
| |
�u�S�̂̑O�Ő�������l�q�v |
|
|
| �܂Ƃ߂� |
�V |
�{���̊w�K���܂Ƃ߂�B |
| |
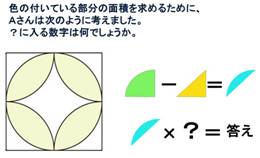
���G�Ȍ`�̖ʐς��A�`�̑g�ݍ��킹�����l����ƁA����܂łɊw�K�����ʐς̌������g���ċ��߂邱�Ƃ��ł���B |
| |
|
�W |
�K�p���������B
|
| |
 |
| |
|
|
�E |
���G�Ȍ`�̖ʐς��A���K�̐}�`��g�ݍ��킹�čl����ƁA���K�̐}�`�̖ʐς̌�����p���ċ��߂��邱�ƂɋC�t������B |
| |
|
�E |
�K�p�����������A�{���̊w�K���e�̒蒅��}��B |
| |
|
�E |
�������s�\���Ȏ����������ꍇ�͑S�̎w�����A���Ȃ��ꍇ�͌ʎw�����s���A�{���̓��e�𗝉�������B |
| |
|
�E |
���Ƃŕ����������Ƃ⊴�z�A���ꂩ��C��t���������Ƃ�X�ɒ��ׂĂ݂������ƂȂǂ���������悤�ɂ���B |
|