
| ホーム | 研究概要 | 授業アイディア | 実践事例 | 参考資料 | 研究事業トップへ |
 |
||||||||||||||
|
||||||||||||||
| 学習問題 | 指導のポイント | 関連のある単元 | |
 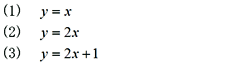 |
・2年の確率の単元末の発展問題として取り扱う。3つの直線のうち、どの直線上に点がくる確率が高いか予想を立てさせる。 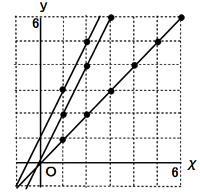 [解答例] 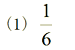 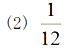  |
一次関数 (中2) 確率(中2) |
|
| Aさんの学校で、運動場に下図のようなトラックをつくることになりました。直線部分の距離は50mで、1レーンのカーブ(半円)の半径はrmです。また、そのレーンの距離は内側の線上を測ることにし、各レーンの幅は1mです。ただし、短距離走ではすべて定められたレーンを走るものとします。 (1)1レーンは1周、何mありますか。 (2)1周の短距離走をするときに、1レーンと2レーンの走者が平等になるようにするには、2レーンのスタート位置は何m先にすればよいでしょうか。 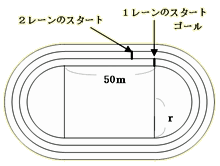 |
・「陸上競技場のセパレートコースを設定する。その時のスタート地点をどのようにして決めるか。」を計算させる。 ・文字の式を利用して、計算で求めさせる。実際は、コースの幅だけがスタート地点の差に影響することを発見させる。 [解答例]  ※1周400mの公式の競技場では、各レーンの幅が、1m22cmです。 |
式の計算 (中2) |
|
    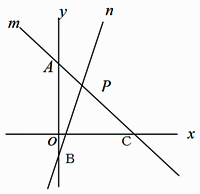 |
・2年生の一次関数の単元末の発展問題として取り扱う。2本の直線と [解答例] 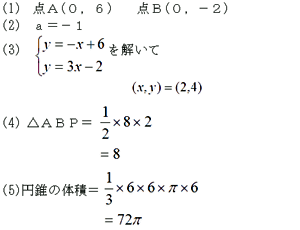 詳しくはこちらをクリック→【中学校 実践事例】 |
一次関数 (中2) 平面図形 (中1) 空間図形 (中1) |
|
| 次の問に答えましょう。 (1)現在、兄は200円、弟は400円の貯金があります。来月から、兄は毎月500円、弟は毎月100円ずつ貯金をしていくことにしました。兄の貯金残高が弟の貯金残高の2倍になるのは何か月後でしょう。(ただし、利子は考えなくてもよいです。) (2)現在、姉は200円、妹は400円の貯金があります。来月から、姉は毎月500円、妹は毎月300円ずつ貯金をしていくことにしました。姉の貯金残高が妹の貯金残高の2倍以上になることはありますか。(ただし、利子は考えなくてもよいです。) (3)(2)において、妹の毎月の貯金額がどういう条件であれば(他の条件はそのまま)、姉の貯金残高が妹の貯金残高の2倍以上になるのか考えましょう。 |
・(1)と(2)は、似たような問題であるが、答えが出るものと出ないものをともに解き、その理由を探る。問題文が読みやすく理解しやすいが、(2)については方程式を立てて解くと答えが負の数になる。 ・活用問題として取り扱うには、 ・(1)の問題をグラフで考えたとすると、 ・(2)の問題をグラフで考えたとすると、 [解答例] (1) 答え 2か月後 (2)2倍以上になることはない (3)250円未満 |
連立方程式 (中2) 一次関数 (中2) 一次方程式 (中1) |
|
縦50cm、横100cm、高さが80cmの直方体の形をしたお風呂があります。次の問いに答えましょう。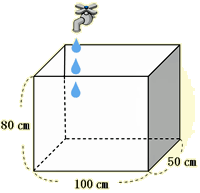 (1)1分間に20リットルの割合でお湯を入れます。入れ始めてからの時間( (2)最初にお風呂にお湯が10cmのところまで入っていました。そこに1分間に40リットルの割合でお湯を入れます。入れ始めてからの時間( (3)ちょうど真ん中に高さが40cmの仕切りを作り、A室とB室に分けました。1分間に20リットルの割合でお湯を入れます。入れ始めてからの時間( 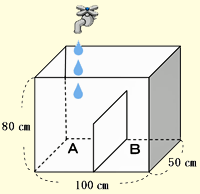 |
・(1)は比例のグラフになり、(2)は一次関数のグラフになる。このようなグラフを何種類か示して、その中から当てはまるグラフを選ばせてもよい。また、そのグラフを選んだ理由も答えさせるようにする。 [解答例] (1) 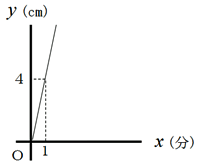 (2) 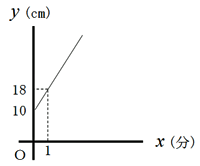 (3) 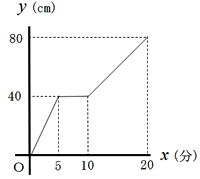 |
一次関数 (中2) |
| Copyright(C) 2008 SAGA Prefectural Education Center. All Rights Reserved. |