���w�I�����������ꂽ���ƓW�J�� |
|
|
|
|
|
�@�P���u�}�`�Ƒ����v�̏��P���u�����Ȑ}�`�v�i�R���ԁj�ɂ����鐔�w�I�����������ꂽ���ƓW�J�Ăł��B |
| |
�P���@�}�`�Ƒ����@�i�[�ъفj
�@�P�@�}�`�Ƒ���
�@�@
�y�E�P�E�@�����Ȑ}�`�z�@�@
�S�R����
|
| |
| |
|
�@
�E�@�ώ@�A�����ʂ��āA�����`�Ƃ͂ǂ̂悤�Ȃ��Ƃ��l���悤�Ƃ���B
�@
�E�@�����`�̐}�`����ɁA�g��E�k���𗝉�����B |
| �i�K |
|
| ���� |
| �� |
���ȏ�106�y�[�W�̎ʐ^�����Ȃ���A�傫��������Ă��Ă������`�ɂȂ��Ă��邱�Ƃ��m�F����B |
| �� |
�{���̊w�K���e�u�`�͓����ő傫�����Ⴄ�}�`�ɂ��Ċw�ڂ��v��m��B |
|
|
| ���ʂ� |
| ���w�I�����@�k���藧������\�z���銈���l |
| �� |
�`�͓����ő傫�����Ⴄ�}�`�̓�����\�z����B |
|
| ���荇�� |
| ���w�I�����@�k�ώ@�A����Ȃǂ̋�̓I�Ȋ����l |
| �� |
���ȏ�10�V�y�[�W�́u�Ƃт�̖��v�Ɏ��g�ށB |
| �� |
���ȏ�107�y�[�W�́u�݂�ȂŘb�������Ă݂悤�v�Ɏ��g�ށB |
| ���w�I�����@�k�����̍l����l�ɓ`���銈���E�l�̍l���𗝉����銈���l |
| �� |
�O���[�v�ŁA�u�Ƃт�̖��v�ł������}�`���ׂāA�����邱�Ƃ��l����B |
|
| �[�߂� |
| ���w�I�����@�k���W�I�ɍl���銈���l |
| �� |
���ȏ�108�y�[�W�̖�P���l����B |
| ���w�I�����@�k�����̍l����l�ɓ`���銈���E�l�̍l���𗝉����銈���l |
| �� |
�O���[�v�ŁA�����̒�����p�̑傫���ɂ��āA�ǂ̂悤�ȓ��������邩��b�������B�܂��A���ȏ�108�y�[�W�̐}�`���ׂāA�����`�łQ�{�̐}�`�ɂȂ��Ă邩�m�F����B |
| �� |
�g��A�k���y�ъg��}�A�k�}�ɂ��Ċm�F����B
| �Q�̐}�`�������āA����̐}�`���g��܂��͏k���������̂ƁA�����̐}�`�������ł���Ƃ��A���̂Q�̐}�`�͑����ł���Ƃ����܂��B |
|
|
| �܂Ƃ߂� |
| ���w�I�����@�k�������s����������U��Ԃ銈���l |
| �� |
���Ƃ�U��Ԃ�A�g��E�k���A�g��}�E�k�}�ɂ��ăm�[�g�ɂ܂Ƃ߂�B |
|
|
�@�@���@�ڍ��ƓW�J�Ăƃ��[�N�V�[�g�ɂ��ẮA�����ȏ��Ή��ł��B |
|
|
�@�E�@�����̊T�O�𖾂炩�ɂ��A�Q�̑����Ȑ}�`���ώ@���āA�����Ȑ}�`�̐������l���邱��
�@
���ł���B
�@�E�@�����̈Ӗ��A�����A������ɂ��ė�������B
|
| �i�K |
|
| ���� |
| �� |
�O���̂܂Ƃ߂���ɁA�����ɂ��Ċm�F����B |
| �� |
�{���̊w�K���e�u�����Ȑ}�`�ɂ��Ċw�ڂ��v��m��B
|
|
|
| ���ʂ� |
| ���w�I�����@�k���藧������\�z���銈���l |
| �� |
�ۑ�P���l����B
���ȏ�109�y�[�W�̗�P�̐}�ŁA��ABC�Ɓ�DEF�͑����ł��B
��ABC�Ɓ�DEF�̑Ή�����ӂ̒�����p�̑傫��������ׂ܂��傤�B
�@�@AB�FDE���i�@�@�F�@�@�j�ABC�FEF���i�@�@�F�@�@�j�ACA�FFD���i�@�@�F�@�@�j
�A�@��A���i�ځ@�@�j�A��B���i�ځ@�@�j�A��C���i�ځ@�@�j�@ |
|
|
| ���荇�� |
| ���w�I�����@�k�ώ@�A����Ȃǂ̋�̓I�Ȋ����l |
| �� |
��K�╪�x��Ȃǂ��g���āA�ӂ̒�����p�̑傫���ׁA�W���m�F����B |
| �� |
�i�@�@�j�ɓ��Ă͂܂�ӂ̔��p���m�F���A�����ȑ��p�`�̐����ɂ��Ă܂Ƃ߂�B
�@�@�Ή���������̒����̔�́A���ׂē������B
�A�@�Ή�����p�̑傫���́A���ꂼ�ꓙ�����B
|
|
| �� |
�L���u |
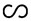 |
�v���g���������Ȑ}�`�̕\������m��B |
| �� |
���ȏ�110�y�[�W�̖�Q���l����B
|
| ���w�I�����@�k�����̍l����l�ɓ`���銈���E�l�̍l���𗝉����銈���l |
| �� |
�O���[�v�Ŋm�F����B |
| �� |
�@�u������v�ɂ��Ēm��B |
| �� |
���ȏ�110�y�[�W�̗�Q�̐������A��������B |
| �� |
�ۑ�Q���l����B
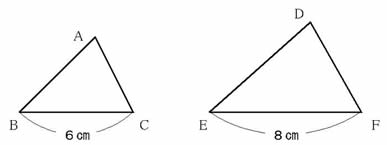
���w���̐}�́�ABC�Ɓ�DEF�͑����ł��B���̂Ƃ��A��ABC�Ɓ�DEF�̑���������߂܂��傤�B�x�ɂ��āA���Y����͑�������u�U�F�W�v�Ɠ����܂����B
���Y����̍l���͐������ł��傤���B
 �@ �@
|
|
| ���w�I�����@�k�����̍l����l�ɓ`���銈���E�l�̍l���𗝉����銈���l |
| �� |
���Y����̍l�������������ǂ��������̍l���\���A�������m�F����B |
|
| �[�߂� |
| ���w�I�����@�k���W�I�ɍl���銈���l |
| �� |
���ȏ�110�y�[�W�̖�R�A��S���l����B |
| ���w�I�����@�k�����̍l����l�ɓ`���銈���E�l�̍l���𗝉����銈���l |
| �� |
�O���[�v�̃����o�[�Ō݂��ɁA�����̍l��������������A�m�F����B |
| �� |
��̒l�ɂ��Ēm��B |
|
| �܂Ƃ߂� |
| ���w�I�����@�k�������s����������U��Ԃ銈���l |
| �� |
���Ƃ�U��Ԃ�A������ɂ��Ă܂Ƃ߂�B |
|
|
|
|
|
�@�E�@�������Ή�����ӂ̒��������߂邱�Ƃ��ł���B |
| �i�K |
|
| ���� |
| �� |
�{���̊w�K���e�u��̐������g���ĕӂ̒��������߂悤�v��m��B |
|
|
| ���ʂ� |
| �� |
�ۑ���l����B
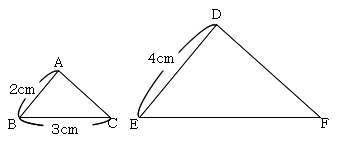
���̐}�ŁA���`�a�b�䁢�c�d�e�ł���Ƃ��A����������߂܂��傤�B
�܂��A�d�e�̒��������߂܂��傤�B
|
|
| ���w�I�����@�k���藧������\�z���銈���l |
| �� |
�d�e�̒��������߂���@��\�z����B |
|
| ���荇�� |
| �� |
��������m�F���A�����Ȑ}�`�̑Ή�����ӂ̔䂪���������Ƃ𗘗p���āA��Ꭾ�ɕ\���ċ��߂邱�Ƃ�m��B |
| �� |
�������m�F����B |
| �� |
�@�u�@a�Fb��c�Fd�@�Ȃ�@ad��bc�@�v�ł��邱�Ƃ��m�F����B |
| �� |
���ȏ�111�y�[�W�̗��P���l����B |
| ���w�I�����@�k�����̍l����l�ɓ`���銈���E�l�̍l���𗝉����銈���l |
| �� |
�O���[�v�̃����o�[�Ō݂��ɁA���ߕ��Ɠ����ɂ��āA�����̍l��������������B |
| �� |
���ߕ��Ɠ������m�F����B |
| �� |
���ȏ�111�y�[�W�̖�T���l����B |
|
| �[�߂� |
| ���w�I�����@�k���W�I�ɍl���銈���l |
| �� |
���ȏ�111�y�[�W�̗��K���P���l����B |
| ���w�I�����@�k�����̍l����l�ɓ`���銈���E�l�̍l���𗝉����銈���l |
| �� |
�O���[�v�̃����o�[�Ō݂��ɁA���ߕ��Ɠ����ɂ��āA�����̍l��������������B |
| �� |
���ߕ��Ɠ������m�F����B |
|
| �܂Ƃ߂� |
| ���w�I�����@�k�������s����������U��Ԃ銈���l |
| �� |
�������m�F���A�ӂ̔�ɂ��ăm�[�g�ɂ܂Ƃ߂�B |
|
|
|
| |
|
| Copyright(C) 2012 SAGA Prefectural Education Center. All Rights Reserved. |
|