過程 |
|
指導上の留意点(・)、評価規準と評価方法(◎○)
算数的活動(◇)、ICT利活用(◆) |
つかむ |
[問題]
下の三角形ABCを2倍に拡大した三角形DEFのかき方を考えましょう。
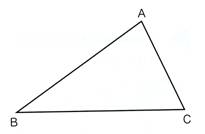 |
|
・ |
前時の学習を振り返り、本時では方眼のます目がないことを確認する。 |
|
|
|
| 見通す |
| 2 |
解決の見通しをもつ。 |
| |

「電子黒板を用いた問題提示の様子」 |
| |
・ |
2倍の拡大図がどんな図になるかイメージする。 |
| |
・ |
三角形の拡大図をかくために必要な情報を考える。 |
|
・ |
作図をする際に、三角形の全ての辺の長さや角の大きさが必要かを問い、合同な三角形をかく場合は、3つの条件が必要だったことを想起させる。 |
| |
|
・ |
これまでの学習を振り返り、既習の合同な三角形のかき方が使えることに気付かせる。 |
| |
|
・ |
最初は、辺BCに対応する辺EFからかき始めることを確認する。 |
|
| 自力解決 |
| 3 |
自力解決をする。 |
| |
三角形の拡大図をかき、その際の作図した手順や既習事項の何を使ったかをノートに書く。 |
| |
《予想される児童の考え》
|
| |
・ |
辺ABと辺ACの長さをそれぞれ2倍にしてコンパスを使って拡大図をかく。 |
| |
・ |
角Bの大きさはそのままにして、辺ABの長さを2倍にして拡大図をかく。 |
| |
・ |
角Bと角Cをそのままにして分度器を使って、拡大図をかく。 |
《児童が実際にノートにかいた考え》
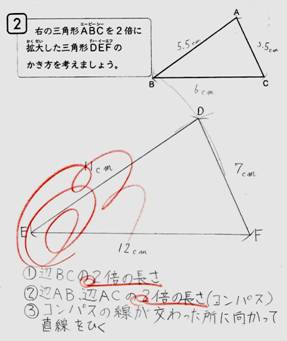 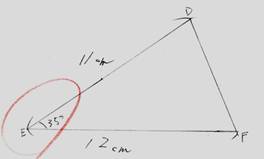
「十分満足できる」状況(A)と判断したノート記述の例
|
・ |
三角形ABCについて、辺の長さと角の大きさが全て記入されているワークシートを用意しておき、必要に応じて配布する。 |
| ◇ |
作図した図には、自分が使った辺の長さ、角の大きさだけを記入させる。(ア) |
| ◇ |
作図した手順が分かるように、作図した図の中に番号を記入させる。 (ア) |
| ◇ |
文章で手順を書く際には、分かりやすいように箇条書きにさせる。 (ア) |
| ◇ |
ノートの吹き出しに、どのような既習事項を使ったかを書かせる。(合同な三角形のかき方や拡大図の性質) (ア) |
・ |
透明シートに三角形ABCを2倍に拡大した三角形DEFを印刷したものを用意しておき、作図した図形と重ね合わせさせ間違っていないかを確かめさせる。 |
・ |
1つの方法で作図できた児童には、他の方法でも作図できないかを考えさせる。 |
| ◆ |
図などが分かりやすく表現できている子どものノートを書画カメラで撮り、発表の準備をさせておく。 |
○ 合同な三角形のかき方を基に、辺の長さや角の大きさに着目して、三角形の拡大図のかき方を考えている。
【数学的な考え方】(観察、ノート)
A 拡大図をかくために必要な辺の長さや角の大きさを測定し、合同な三角形のかき方と関連付けて、2倍の拡大図のかき方を2つ以上の方法で考えている。
B 拡大図をかくために必要な辺の長さや角の大きさを測定し、2倍の拡大図のかき方を1つの方法で考えている。
〔「努力を要する」状況(C)と判断した児童への指導〕
もとの三角形の2倍の長さの底辺をひいて、他に必要な辺の長さや角の大きさを考えさせる。
|
| ※ |
「努力を要する」状況(C)である児童が「おおむね満足できる」状況(B)となるよう指導し、「十分満足できる」状況(A)の児童がいれば記録に残す。 |
|
| 学び合い |
|
・ |
作図した図形や、書き込んだことを基に手順を説明する。 |

「手順を示しながら説明しあっている様子」 |
| ◇ |
小集団で、作図の手順が分かるように「まず、次に…」といった順序を表す言葉を使って説明させる。(イ) |
| |
|
・ |
どのような既習事項を活用しているのかを意識して聞かせる。 |
|
5 |
考えたことをグループの代表が発表し、全体で話し合う。 |
|
| ◆ |
書画カメラを用いて児童のノートを拡大提示し、その図形を使ってかき方の手順を説明させる。 |
| |
|
・ |
拡大図のかき方について、「3つの辺の長さ」「2つの辺とその間の角」「1つの辺とその両端の角」の3通りの方法を説明させる。 |
| |
|
|
・ |
既習事項の何を使ったかを問い、合同な三角形のかき方や拡大図の性質を活用していることを確認し、板書する。 |
|
| まとめる |
|
合同な三角形のかき方を使うと拡大図や縮図をかくことができる。 |
[問題]
三角形ABCの1/2の縮図をかきましょう。
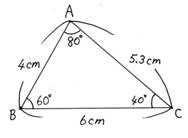
|
8 |
本時の学習を算数日記にまとめる。 |
| |
《児童が実際に書いた算数日記の例》 |
|
・ |
三角形の拡大図をかく際には、拡大図の性質や合同な三角形のかき方を使えばかけることをまとめる。 |
・ |
3つの辺の長さと角の大きさが分かっている三角形ABCの1/2の縮図を、拡大図のかき方を基にワークシートにかかせる。 |
・ |
まずは辺BCを1/2の長さでかかせ、次にどの情報が必要か板書を参考にしながら考えさせる。 |
・ |
辺ACの長さが小数であることから、辺ACを使わずに作図する方法(「2つの辺とその間の角」「1つの辺とその両端の角」)のよさに気付くことができるようにする。 |
◎ 三角形の拡大図のかき方を基に、必要な辺の長さや角の大きさに着目して、縮図をかくことができる。
【技能】(観察、ワークシート)
A 辺ACの長さが小数であることに着目して、3通りの作図の仕方の中から「2つの辺とその間の角」や「1つの辺とその両端の角」を使った方法を選択し、正確に縮図をかくことができる。
B 合同な三角形のかき方と関連付けて、縮図をかくことができる。
〔「努力を要する」状況(C)と判断した児童への指導〕
拡大図をかくときに用いた合同な三角形のかき方を想起させ、1/2の長さの底辺をひいて、他に必要な辺の長さや角の大きさを確認する。
|
| ※ |
学習活動の観察や授業後のワークシートの記述の分析を基に、全員を対象とした評価を行い記録に残す。 |
・ |
授業で分かったことや感想、これから気を付けたいことや更に調べてみたいことなどを書かせるようにする。 |
|







