過程 |
|
指導上の留意点(○)、評価規準と評価方法(◇)
算数的活動(◎) |
|
つかむ |
[問題]
牛乳とコーヒーの量の比を20:50にして、コーヒー牛乳をつくります。
コーヒーが1800mLあります。牛乳は、どれだけ必要になりますか。 |
|
| ○ |
コーヒーを基にして、前時の課題と同じ味のコーヒー牛乳を作るために、どんなことが分かればよいか考えさせる。
|
| ○ |
準備物…牛乳、市販のボトル入りコーヒー、やかん、
第1時と同じ割合で作ったコーヒー牛乳
プラスチックコップ(児童用・教師用) |
|
コーヒーを基にして前時と同じ味のコーヒー牛乳をつくろう |
|
見通す |
2 |
解決の見通しをもつ。 |
| |
・ |
コーヒーの量を基にして考える。
(比べる量)÷(基にする量)=(割合)
|
|
| ○ |
(比べる量)÷(基にする量)=(割合)の考え方をいかすことを気付かせるために、前時にどのようにして解決したかを振り返らせる。 |
|
| 自力解決 |
3 |
自力解決をする。 |
| |
《予想される児童の考え》 |
| |
① |
式で表す。
コーヒーを基にすると牛乳は
20÷50=0.4 答え 0.4倍
1800×0.4=720 答え 720mL
|
| |
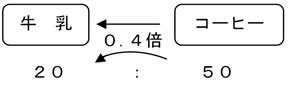
② |
図で示す。
|
| |
③ |
50のうちの1の割合を求める。
1800÷50=36 (比の1にあたる量)
36×20=720 答え 720mL |
|
| ○ |
前時は、割合の考えから比の考えへと関連付けているが、本時では、比20:50から割合の考えへと関連付けて考えさせる。 |
| ◎ |
この後の学び合いの活動で友達に説明させるために、ノートに図、式、言葉などを用いて記述するようにさせる。(ア) |
|
| 学び合い |
4 |
自分の考えをグループでお互いに説明し合う。 |
|
「理由を指し示しながら説明し合っている様子」 |
|
| ◎ |
自分の考えを説明する際には、ノートを示しながら説明させる。(ア) |
| ◎ |
自分の考えを説明させる際には、児童が発言する次のような言葉に注目し、児童の考えをつなげていく。 (ア) |
| |
・まず…自分の考えを分割し、整理しようする言葉。
・でも…反例をあげ、考えを説明しようとする言葉。
・だったら…友達の考えを基にして、その先を考えて
説明しようとする言葉。
・もし…条件を変えたり、考えを整理したり、一般化
を図ったりしようとする言葉。 |
| ◎ |
これまでの学習を基に、言葉や図、式などを関連付けて説明させる。(ア) |
| ◎ |
自分のやり方と同じか違うかを意識させながら聞かせる。また、よく分からないところは、お互いに質問し合わせる。(ア) |
| ◎ |
説明を聞いて、自分の考えと異なる考えやよい考えがあったらノートにかかせる。(ア) |
◇ 比の表し方を基にして割合を求め、割合と比の値を関連付けて考えている。
【数学的な考え方】[ノート、行動観察] |
|
5 |
考えたことをグループの代表が発表・板書し、全体で話し合う。
|
| |
≪児童が実際にノートにかいた考え≫ |
|
「③の考えを表現しているノート例」
|
| |
・ |
比の値の意味を知る。
「a : b の比の値は a÷b で求められる」 |
| |
|
「a: b の比の値 |
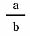 |
は、a が b の何 |
| |
|
倍になっているかを表す数」(割合) |
| |
・ |
話し合いで導き出した割合でコーヒー牛乳を作る。 |
|
| ◎ |
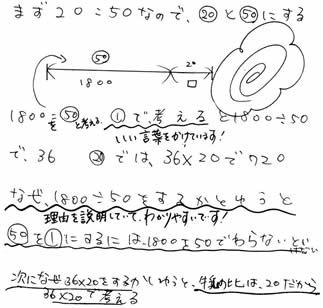
左の児童のノート例では、
図、式、言葉を使って考えたことを根拠を明らかにして説明している。
その際、左の例にあるような「まず」「次に」「なぜ~かというと」「~だから」などの言葉を積極的に使わせ、根拠を明らかにして筋道立てて説明させる。
(ア)
|
| ○ |
コーヒーの量(もとにする量)に比の値(割合)をかけることで、牛乳の量(比べる量)が求められることを確認する。コーヒー牛乳は、教師が全員分をまとめて作り、配布する。 |
| ◎ |
前時の課題と同じ割合で、事前に作っておいたコーヒー牛乳をグループ毎に配布する。児童には、自分用のコップを準備させておく。できるだけ、本時で作ったコーヒー牛乳と同じくらいの温度にすると、よりはっきりと味を感じることができる。(イ) |
|
| まとめる |
6 |
本時の学習をまとめる。 |
| |
・ |
比の表し方から割合を求めることができる。 |
| |
・ |
前時の課題と同じ割合で作っておいたコーヒー牛乳と本時で作ったコーヒー牛乳を飲み比べ、混ぜた比が同じであったかどうかを味で確認する。
|
| 7 |
振り返り問題を解く。(教科書p.63 ②③④)
|
| 8 |
本時の学習を算数日記にまとめる。 |
| ≪児童が実際に書いた算数日記の例≫ |
 |
|
| ○ |
前時は、割合の考えから比の考えへと関連付けているが、本時では、比20:50から割合の考えへと関連付けて考えさせたことで、比と割合は相互に関連付けて考えられることを確認する。 |
| ◎ |
身近な日常生活の場面で、比の値を使うよさに気付かせ、学んだことが生活にいかせることを体験させる。(イ) |
◇ 比の値を求めることができる。
【数量や図形についての技能】[ノート、行動観察] |
| ○ |
授業で分かったことや感想、これから気を付けたいことやさらに調べてみたいことなどを書かせるようにする。 |
|