過程 |
学習活動
|
指導上の留意点(・)、評価規準と評価方法(◎○)
算数的活動(◇)、ICT利活用(◆) |
つかむ |
1 前時の学習を振り返る。
2 本時の課題を捉える。
| |
|
|
| |
・ |
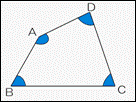
四角形の4つの角の大きさの和が何度になるか考える。 |
|
| ◆ |
電子黒板を用いて、いろいろな三角形を示し、三角形の内角の和が180°であることを確認する。 |
・ |
正方形と長方形を提示して、4つの角の大きさの和が360°になることを確認し、他の四角形の場合はどうかを予想させる。 |
|
角度を測らないで、4つの角の大きさの和を求める方法を考えよう。 |
|
見通す |
3 解決の見通しをもつ。 |
・ |
四角形を三角形に分けることができたら、三角形の内角の和を基にして考えられることに気付かせる。 |
|
自力解決 |
4 自力解決をする。
| |
・ |
各自が考えた方法で、内角の和を調べる。 |
| |
|
|
| |
《予想される児童の考え》 |
| |
・ |
4つの角を切って1点に集める。 |
| |
・ |
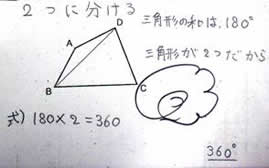
三角形2つに分ける。 |
| |
・ |
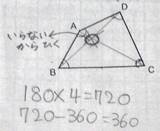
三角形4つに分ける。 |
| |
|
|
| |
|
|
| |
|
「十分満足できる」状況(A)と判断したノート記述の例 |
|
| ◇ |
式だけでなく図や言葉を使って、方法と理由が分かるようにノートにかき表させる。(ア) |
・ |
前時のように角を切って集めたり、敷き詰めたりして確かめることも認める。 |
・ |
対角線で2つの三角形に分けて解決できた児童には、いくつかの三角形に分ける方法でも解決できるか考えさせる。 |
◎ 三角形の内角の和を基に、四角形の内角の和の求め方を演繹的に考え、説明している。
【数学的な考え方】(観察、ノート)
A 四角形を対角線や直線でいくつかの三角形に分けて、三角形のいくつ分かを基に多様な方法で考え、記述している。
B 四角形を対角線で三角形に分けて、三角形の2つ分であることを基に考え、記述している。
〔「努力を要する状況(C)と判断した児童への指導〕
四角形を対角線で2つの三角形に分けて、三角形の内角の和が180°であることを基に、その2つ分で何度になるか考えさせる。
|
※ |
学習活動の観察や授業後のノート記述の分析を基に、全員を対象とした評価を行い記録に残す。 |
|
学び合い |
5 |
ペアや全体でそれぞれの考え方を発表し、話し合う。 |
| |
|
| |
「全体の前で説明する様子」 |
四角形の4つの角の大きさの和は、三角形に分けると求められる。
四角形の4つの角の大きさの和は、360°になる。 |
|
◇ |
図と式を結び付けて、ペア学習の相手に根拠を明らかにして説明させる。(イ) |
| |
|
| ◆ |
書画カメラを用いて児童のノートを拡大提示し、その図を使って説明させる。 |
| |
|
◇ |
全体の場で、四角形をどのように三角形に分けて考えたのかを明らかにさせ、どの考え方も三角形の内角の和が180°であることを用いて求めていることに気付かせる。(イ) |
|
6 適用問題を解く。
| |
・ |
違う形の四角形も「4つの角の大きさの和が360°になる」理由を説明し合う。 |
| |
|
|
| |
・ |
早く解決ができた児童は、教科書p7[2]の問題を解く。 |
|
| ◇ |
対角線で2つに分けて説明できた児童には、他の分け方でも考えさせる。(イ) |
※ |
適用問題においても、本時の評価規準に照らして評価を行い、自力解決で「努力を要する」状況(C)であった児童が、授業を通して内角の和の求め方を理解し解決できていれば、「おおむね満足できる」状況(B)と評価する。
|
|
まとめ |
8 本時の学習を振り返り、算数日記を書く。 |
・ |
授業で分かったことや感想、これから気を付けたいことや更に調べてみたいことなどを書かせるようにする。 |
|