���w�I�����������ꂽ���ƓW�J�� |
|
|
|
|
|
�@�P���u�O�����̒藝�v�̏��P���u���ʐ}�`�ւ̗��p�v�i�R���ԁj�ɂ����鐔�w�I�����������ꂽ���ƓW�J�Ăł��B |
| |
�P���@�O�����̒藝�@�i�[�ъفj
�@�Q�@�O�����̒藝�̗��p
�@�@
�y�E�P�E�@���ʐ}�`�ւ̗��p�z�@�@
�S�R����
|
| |
| |
|
�@�E�@���ʐ}�`�̒��ɒ��p�O�p�`�����������A�O�����̒藝��p���ĉ�@�����ʂ����Ƃ��ł�
�@
��B
�@�E�@���O�p�`�Ȃǂ̍�����ʐς��A�O�����̒藝���g���ċ��߂邱�Ƃ��ł���B
|
| �i�K |
|
| ���� |
| �� |
�O�����̒藝�ɂ��Ċm�F����B |
| �� |
�{���̊w�K���e�u�O�����̒藝�𗘗p���āA�����̒�����ʐς����߂悤�v��m��B |
|
|
| ���ʂ� |
| ���w�I�����@�k���藧������\�z���銈���l |
| �� |
�ۑ�P���l����B
| �P�ӂ̒�����10 �p �̐��O�p�`�̖ʐς����߂悤�B |
|
| �� |
�O�p�`�̖ʐς̋��ߕ��ɂ��Ċm�F����B |
| �� |
�����̋��ߕ��ɂ��čl����B |
|
| ���荇�� |
| ���w�I�����@�k�����̍l����l�ɓ`���銈���E�l�̍l���𗝉����銈���l |
| �� |
�O���[�v�ŁA�����̋��ߕ��ɂ��āA�����̍l��������������B |
| �� |
�����̋��ߕ��Ɠ����A�ʐςɂ��Ċm�F����B |
| �� |
���������߂邽�߂ɁA���O�p�`�̒��ɕ\�������p�O�p�`���A60���A30���̒��p�O�p�`�ŁA�O�p��K�Ƒ����ɂȂ��Ă��邱�ƂɋC�t���B |
| �� |
�����`�ɑΊp�����Ђ��A�����ɕ\�����O�p�`�����p�ӎO�p�`�ł��邱�Ƃ𗝉�����B |
| �� |
�ۑ�Q���l����B
���̂Q�̒��p�O�p�`��3�ӂ̒����̊��������߂悤�B
�@�@60���A30���̊p�������p�O�p�`
�A�@���p�ӎO�p�` |
|
| ���w�I�����@�k�����̍l����l�ɓ`���銈���E�l�̍l���𗝉����銈���l |
| �� |
�O���[�v�ŁA�R�ӂ̒����̊����Ƃ��̍l�����ɂ��āA�����̍l��������������B |
| �� |
���ꂼ��̒��p�O�p�`���A���̕ӂ̒����̊����ɂȂ邱�Ƃ𗝉�����B |
| |
�@�̏ꍇ�@ |
�P �F �Q �F |
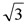 |
�A�̏ꍇ�@ |
�P �F �P �F |
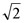 |
|
| �[�߂� |
| ���w�I�����@�k���W�I�ɍl���銈���l |
| �� |
�ۑ�R���l����B
���̎O�p�`�̖ʐς����߂悤�B
�@�@�P�ӂ̒������W�p�̐��O�p�`
�A�@�������Q�ӂ��U�p�A��ӂ��W�p�ł���ӎO�p�` |
|
| �� |
�����̍l���\����B |
| �� |
�����Ƃ��̋��ߕ����m�F����B |
|
| �܂Ƃ߂� |
| ���w�I�����@�k�������s����������U��Ԃ銈���l |
| �� |
�{���̊w�K��U��Ԃ�A�O�����̒藝�̗p��������ʂȒ��p�O�p�`�̕ӂ̒����̊����ɂ��Ċm�F����B |
|
|
|
|
|
�@�E�@���̒������A�O�����̒藝���g���ċ��߂邱�Ƃ��ł���B
�@�E�@���ʐ}�`�ɂ����ĎO�����̒藝���g���Ē��������߂����ʂ𗝉�����B |
| �i�K |
|
| ���� |
| �� |
�{���̊w�K���e�u�O�����̒藝�𗘗p���āA���̒������߂悤�v��m��B |
|
|
| ���ʂ� |
| ���w�I�����@�k���藧������\�z���銈���l |
| �� |
���ȏ�124�y�[�W�̗��Q�̋��ߕ����l����B |
| �� |
���ߕ����m�F����B |
|
| ���荇�� |
| ���w�I�����@�k�ώ@�A����Ȃǂ̋�̓I�Ȋ����l |
| �� |
���Q�̐}���Q�l�ɂ��Ȃ���A���������}���m�[�g�ɂ����B |
| �� |
�������}�ɁA���aOA���P�ӂɂ����p�O�p�`���������݁A���̔���(AH)�̒������l����B |
| ���w�I�����@�k�����̍l����l�ɓ`���銈���E�l�̍l���𗝉����銈���l |
| �� |
�������}���g���āA�O���[�v�ŋ��ߕ��Ɠ����ɂ��āA�����̍l��������������B |
| �� |
�����̍l���\����B |
| �� |
���ߕ��Ɠ������m�F����B |
| �� |
���ȏ�124�y�[�W�̖�S���l����B |
| �� |
���ߕ��Ɠ����\����B |
| �� |
�������m�F����B |
|
| �[�߂� |
| ���w�I�����@�k���W�I�ɍl���銈���l |
| �� |
�ۑ���l����B
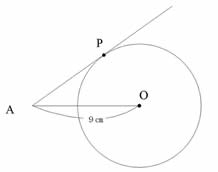
���a�U�p�̉~O�ƁA���S����X�p���ꂽ�_�`������܂��B
�_�`����~O�ɐڐ����Ђ��A���̐ړ_���o�Ƃ��܂��B
���̂Ƃ��A�����`�o�̒��������߂Ȃ����B
|
|
| ���w�I�����@�k�����̍l����l�ɓ`���銈���E�l�̍l���𗝉����銈���l |
| �� |
�O���[�v�ŁA����AP�̋��ߕ��ɂ��āA�����̍l��������������B |
| �� |
���aO�o���Ђ��A��PAO�����p�O�p�`�ł��邱�Ƃ��m�F����B |
| �� |
AP�̒��������߂�B |
|
| �܂Ƃ߂� |
| ���w�I�����@�k�������s����������U��Ԃ銈���l |
| �� |
�g�����}�Ƌ��ߕ���U��Ԃ�Ȃ���A�O�����̒藝���m�F����B |
|
|
|
|
|
�@�E�@�Q�_�Ԃ̋������A�O�����̒藝���g���ċ��߂邱�Ƃ��ł���B
�@�E�@���ʐ}�`�ɂ����ĎO�����̒藝���g���Ē��������߂����ʂ𗝉�����B |
| �i�K |
|
| ���� |
| �� |
�{���̊w�K���e�u�O�����̒藝�𗘗p���āA�Q�_�Ԃ̋��������߂悤�v��m��B |
|
|
| ���ʂ� |
| ���w�I�����@�k���藧������\�z���銈���l |
| �� |
���ȏ�125�y�[�W�̗��R�̋��ߕ����l����B |
| �� |
���ߕ����m�F����B |
|
| ���荇�� |
| ���w�I�����@�k�ώ@�A����Ȃǂ̋�̓I�Ȋ����l |
| �� |
�Q�_�̍��W���Ƃ�A���̂Q�_�����Ԑ������P�ӂɂ����p�O�p�`���������݁A�����̒������l����B�i���O���t�p������������B�j |
| ���w�I�����@�k�����̍l����l�ɓ`���銈���E�l�̍l���𗝉����銈���l |
| �� |
�������}���g���āA�O���[�v�Ő����̒����̋��ߕ��Ɠ����ɂ��āA�����̍l��������������B |
| �� |
�����̍l���\����B |
| �� |
���ߕ��Ɠ������m�F����B |
| �� |
�Q�_�Ԃ̋����́A�Q�_�����Ԑ������ΕӂƂ��A���W���ɕ��s�ȂQ�̕ӂ������p�O�p�`�����邱�Ƃ𗝉�����B |
| �� |
���ȏ�125�y�[�W�̖�T���l����B |
| �� |
���ߕ��Ɠ������m�F����B |
|
| �[�߂� |
| ���w�I�����@�k���W�I�ɍl���銈���l |
| �� |
���ȏ�130�y�[�W�͖̏����S���l����B |
| ���w�I�����@�k�����̍l����l�ɓ`���銈���E�l�̍l���𗝉����銈���l |
| �� |
�O���[�v�ŁA���ߕ��Ɠ����ɂ��āA�����̍l��������������B |
| �� |
�����̍l���\����B |
| �� |
���߂��R�ӂ̒�������ɁA�ǂ�ȎO�p�`�ɂȂ邩�m�F����B |
|
| �܂Ƃ߂� |
| ���w�I�����@�k�������s����������U��Ԃ銈���l |
| �� |
���R�̋��ߕ���U��Ԃ�Ȃ���A�O�����̒藝���m�F����B |
|
|
|
| |
|
| Copyright(C) 2012 SAGA Prefectural Education Center. All Rights Reserved. |
|