単元「図形と相似」の小単元「平行線と線分の比」（５時間）における数学的活動を取り入れた授業展開案です。

単元　図形と相似　（啓林館）
　２　平行線と線分の比
　　 【・１・　平行線と線分の比】　　 全５時間

１／５時	ねらい	・　平行線と線分の比に関する性質を理解する。 　・　平行線と線分の比の性質を利用して、辺の長さを求めることができる。
	段階 学習活動【数学的活動を通した指導のポイント】（●は数学的活動をともなう学習活動） つかむ ○ 本時の学習内容「平行線と線分の比の関係について学ぼう」を知る。 見通す 数学的活動　〔成り立つ事柄を予想する活動〕 ● 教科書104ページの「考えてみよう」に取り組む。 練り合う 数学的活動　〔自分の考えを人に伝える活動・人の考えを理解する活動〕 ● グループで、△APQと△ABCが相似になることの証明を話し合う。 ● グループの考えを発表し、証明を確認する。 ○ 相似になることから、AQ、PQの長さを確認する。 ○ 平行線と線分の比についてまとめる。 △ABCの辺AB、AC上に、それぞれ、点P、Qがあるとき、 PQ//BCならば、 AP：AB＝AQ：AC＝PQ：BC ○ 教科書104ページの問１を考える。 数学的活動　〔自分の考えを人に伝える活動・人の考えを理解する活動〕 ● グループのメンバーで互いに、値の求め方について、自分の考えを説明し合う。 深める 数学的活動　〔発展的に考える活動〕 ● グループで、教科書105ページの問２を話し合う。 ○ グループの考えを発表し、証明を確認する。 まとめる 数学的活動　〔自分が行った活動を振り返る活動〕 ● 平行線と線分の比についてノートにまとめる。

２／５時	ねらい	・　平行線と線分の比に関する性質を理解する。 　・　平行線と線分の比の性質を利用して、辺の長さを求めることができる。
	段階 学習活動【数学的活動を通した指導のポイント】（●は数学的活動をともなう学習活動） つかむ ○ 前時のまとめを基に、平行線と線分の比の性質について確認する。 ○ 本時の学習内容「平行線と線分の比の関係について学ぼう」を知る。 見通す 数学的活動　〔成り立つ事柄を予想する活動〕 ● 課題を考える。 △ABCの辺AB、AC上に、それぞれ、点P、Qがあるとき、 PQ//BCならば、AP：PB＝AQ：QCであることを証明しましょう。 練り合う 数学的活動　〔観察、操作などの具体的な活動〕 ● △ABCをノートにかき、課題の条件を確認する。 数学的活動　〔自分の考えを人に伝える活動・人の考えを理解する活動〕 ● グループで、証明を話し合う。 ● グループの考えを発表し、証明を確認する。 ○ 教科書106ページのまとめを基に、平行線と線分の比についてまとめる。 深める 数学的活動　〔発展的に考える活動〕 ● 教科書106ページの問３を考える。 数学的活動　〔自分の考えを人に伝える活動・人の考えを理解する活動〕 ● グループで、答えと求め方を確認する。 まとめる 数学的活動　〔自分が行った活動を振り返る活動〕 ● 平行線と線分の比についてのまとめを基に、比の考え方について確認する。

３／５時	ねらい	・　平行線と線分の比の性質を使って証明を考えることができる。 　・　平行線と線分の比の性質を利用して、辺の長さを求めることができる。
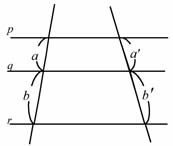
	段階 学習活動【数学的活動を通した指導のポイント】（●は数学的活動をともなう学習活動） つかむ ○ 前時のまとめを基に、平行線と線分の比について確認する。 ○ 本時の学習内容「平行線と線分の比を使って証明しよう」を知る。 見通す 数学的活動　〔成り立つ事柄を予想する活動〕 ● 教科書106ページの例題１を考える。 練り合う 数学的活動　〔観察、操作などの具体的な活動〕 ● 条件を満たす図をかき、証明を考える。 数学的活動　〔自分の考えを人に伝える活動・人の考えを理解する活動〕 ● グループで、証明を話し合う。 ● グループの考えを発表し、証明を確認する。 ○ 例題１の証明を基に、 　 直線 p、q、r が平行のとき、 　　a：b＝a'：b'   　  a：a'＝b：b' が成り立つことの説明を聞き、理解する。 深める 数学的活動　〔発展的に考える活動〕 ● 教科書107ページの問４、問５を考える。 数学的活動　〔自分の考えを人に伝える活動・人の考えを理解する活動〕 ● グループのメンバーで互いに、対応している辺や求め方について、自分の考えを説明し合い、答えを確認する。 まとめる 数学的活動　〔自分が行った活動を振り返る活動〕 ● 平行線と線分の比についてノートにまとめる。

４ ／ ５ 時	ねらい	・　「線分の比と平行線」が「平行線と線分の比」の逆になっていることを理解する。
	段階 学習活動【数学的活動を通した指導のポイント】（●は数学的活動をともなう学習活動） つかむ ○ 教科書106ページの平行線と線分の比のまとめを基に、 　 PQ//BCならば、AP：AB＝AQ：ACであることを確認する。 ○ 本時の学習内容「線分の比と平行線の関係を学ぼう」を知る。 見通す 数学的活動　〔成り立つ事柄を予想する活動〕 ● AP：AB＝AQ：ACならば、PQ//BCが成り立つか予想する。 練り合う ○ 教科書108ページの問６を考える。 数学的活動　〔自分の考えを人に伝える活動・人の考えを理解する活動〕 ● グループで、証明を話し合う。 ● グループの考えを発表し、証明を確認する。 深める 数学的活動　〔発展的に考える活動〕 ● 教科書108ページの問７を考える。 数学的活動　〔観察、操作などの具体的な活動〕 ● 各辺の長さを用いて、AP：AB＝AQ：ACを調べる。 ○ AP：AB＝AQ：ACからPQ//BCが成り立つことを理解する。 まとめる 数学的活動　〔自分が行った活動を振り返る活動〕 ● 授業を振り返り、線分の比と平行線についてノートにまとめる。

５ ／ ５ 時	ねらい	・　「線分の比と平行線」が「平行線と線分の比」の逆になっていることを理解する。 　・　線分の比と平行線の性質を利用して、問題を解決することができる。
	段階 学習活動【数学的活動を通した指導のポイント】（●は数学的活動をともなう学習活動） つかむ ○ 本時の学習内容「線分の比と平行線の性質を利用して、問題を解決しよう」を知る。 ○ 前時の証明を基に、線分の比と平行線の性質を復習する。 見通す ○ 教科書109ページを基に、線分の比と平行線についてまとめる。 練り合う ○ 教科書109ページの問８を考える。 数学的活動　〔観察、操作などの具体的な活動〕 ● 条件を満たす図をかき、その図を基に△ABCと△A'B'C'が相似になるわけを考える。 数学的活動　〔自分の考えを人に伝える活動・人の考えを理解する活動〕 ● グループのメンバーで互いに、相似になるわけについて、自分の考えを説明し合う。 ○ 自分の考えを発表する。 ○ １つの点を中心として、いろいろな図形の拡大図や縮図をかくことができることを知る。 深める 数学的活動　〔発展的に考える活動〕 ● 教科書109ページの問９を考える。 ○ グループで、図を確認する。 まとめる 数学的活動　〔自分が行った活動を振り返る活動〕 ● 線分の比と平行線についてのまとめを振り返り、線分の比と平行線の関係を確認する。