単元「 関数 y ＝ a x ²」の小単元「関数 y ＝ a x ² のグラフ」（４時間）における数学的活動を取り入れた授業展開案です。

単元　関数 y ＝ a x ²　（啓林館）

　１　関数とグラフ

　　【・２・　関数 y ＝ a x ² のグラフ】　　 全４時間

１ ／ ４ 時	ねらい	・　関数 y ＝ a x 2のグラフの特徴をとらえることができる。 　・　関数 y ＝ a x 2のグラフをかくことができる。
	段階 学習活動【数学的活動を通した指導のポイント】（●は数学的活動をともなう学習活動） つかむ ○ 本時の学習内容「関数 y ＝ a x 2をグラフに表し、その特徴を調べよう」を知る。 ○ 教科書71ページの「考えてみよう」に取り組む。 見通す 数学的活動　〔成り立つ事柄を予想する活動〕 ● どんなグラフになるか予想する。 ○ 教科書71ページの問１を考える。 ○ 課題を予想する。 原点近くのグラフはどのようになるか考えてみましょう。 練り合う ○ 自分の考えを発表する。 数学的活動　〔観察、操作などの具体的な活動〕 ● 教科書71ページの問２を考える。 ○ グループで、自分のかいたグラフについて確認する。 ○ 教科書75ページのグラフを基に、関数 y ＝ x 2のグラフを確認する。 深める 数学的活動　〔自分の考えを人に伝える活動・人の考えを理解する活動〕 ● グループで、関数 y ＝ x 2のグラフの特徴を話し合う。 数学的活動　〔目の前の課題から、物事の本質を見抜こうとする活動〕 ● グループの考えを発表し、グラフの特徴について考える。 ○ 関数 y ＝ x 2のグラフの特徴をまとめる。 　・　y軸を対称の軸として線対称である。 　・　原点を通り、x軸の上側にある。 まとめる 数学的活動　〔自分が行った活動を振り返る活動〕 ● 関数 y ＝ x 2のグラフとグラフの特徴を振り返り、ノートに整理する。

２／４時	ねらい	・　関数 y ＝ a x 2（a＞０）のグラフの特徴をとらえることができる。 　・　関数 y ＝ a x 2（a＞０）のグラフをかくことができる。
	段階 学習活動【数学的活動を通した指導のポイント】（●は数学的活動をともなう学習活動） つかむ ○ 前時のまとめを基に、関数 y ＝ x 2のグラフの特徴を思い出す。 ○ 本時の学習内容「関数 y ＝ a x 2（a＞０）をグラフに表し、その特徴を調べよう」を知る。 見通す ○ 教科書72ページの「考えてみよう」に取り組む。 ○ 表とグラフを確認する。 練り合う 数学的活動　〔観察、操作などの具体的な活動〕 ● 教科書75ページのグラフに(２，０)を通り、y軸に平行な直線をひく。 数学的活動　〔成り立つ事柄を予想する活動〕 ● 課題を考える。 教科書73ページのグラフで、関数 y ＝ x 2のグラフ上の点P(２，４)と、 関数 y ＝ ２ x 2 のグラフ上の点P’(２，８)について、どんなことがいえますか。 ○ 自分の考えを発表する。 ○ 教科書73ページの問３を考える。 ○ グループでグラフを確認する。 数学的活動　〔自分の考えを人に伝える活動・人の考えを理解する活動〕 ● グループで、グラフの特徴について話し合う。 ○ x が同じ値のとき、 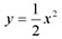の y の値は、 y ＝ x 2 の y の値の  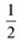 になることを確認する。 深める 数学的活動　〔発展的に考える活動〕 ● 教科書75ページのグラフに、関数 y ＝ ３ x 2 のグラフをかき、x が同じ値のときの y ＝ x 2 の y の値との関係を考える。 数学的活動　〔自分の考えを人に伝える活動・人の考えを理解する活動〕 ● グループでグラフを確認し、 y の値について話し合う。 まとめる 数学的活動　〔自分が行った活動を振り返る活動〕 ● ２つの関数 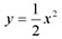と y ＝ x 2 のグラフの y の値の関係を振り返り、   関数 y ＝ a x 2（a＞０）のグラフの特徴をノートに整理する。

３／４時	ねらい	・　関数 y ＝ a x 2（a＜０）のグラフの特徴をとらえることができる。 　・　関数 y ＝ a x 2（a＜０）のグラフをかくことができる。
	段階 学習活動【数学的活動を通した指導のポイント】（●は数学的活動をともなう学習活動） つかむ ○ グラフ用紙に関数 y ＝ x 2のグラフをかく。（※グラフ用紙を準備する。） ○ 本時の学習内容「関数 y ＝ a x 2（a＜０）をグラフに表し、その特徴を調べよう」を知る。 見通す 数学的活動　〔成り立つ事柄を予想する活動〕 ● 教科書73ページの「考えてみよう」に取り組む。 ○ 気付いたことを発表する。 練り合う 数学的活動　〔観察、操作などの具体的な活動〕 ● 関数 y ＝ − x 2のグラフをグラフ用紙にかく。 ○ ２つの関数 y ＝ x 2と y ＝− x 2のグラフを比べ、 関数 y ＝− x 2のグラフの特徴を考える。 数学的活動　〔自分の考えを人に伝える活動・人の考えを理解する活動〕 ● グループのメンバーで互いに、関数 y ＝− x 2のグラフの特徴について、自分の考えを説明し合う。 ○ 関数 y ＝− x 2のグラフの特徴を発表する。 ○ 関数 y ＝− x 2のグラフの特徴をまとめる。 　・　y軸を対称の軸として線対称である。 　・　原点を通り、x軸の下側にある。 深める ○ 教科書74ページの問４を考える。 数学的活動　〔発展的に考える活動〕 ● 課題を考える。 教科書74ページの問４のグラフからどんなことがいえますか。 数学的活動　〔自分の考えを人に伝える活動・人の考えを理解する活動〕 ● グループで、２つのグラフについての特徴を確認する。 ○ グループの考えを発表する。 まとめる 数学的活動　〔自分が行った活動を振り返る活動〕 ● グラフやまとめを基に、関数 y ＝ a x 2のグラフやその特徴をノートに整理する。

４ ／ ４ 時	ねらい	・　放物線、放物線の軸、放物線の頂点の意味を理解する。
	段階 学習活動【数学的活動を通した指導のポイント】（●は数学的活動をともなう学習活動） つかむ ○ 前時にかいたグラフを見ながら復習する。 ○ 本時の学習内容「放物線、放物線の軸、放物線の頂点について知ろう」を知る。 見通す ○ 教科書76ページの６つのグラフについて、x＝１のときの y の値を調べ、aの値と一致することを確認する。 練り合う ○ 「放物線」について知る。 ○ 放物線が、線対称な図形であることを確認する。 ○ 「放物線の軸」、「放物線の頂点」について知る。 数学的活動　〔目の前の課題から、物事の本質を見抜こうとする活動〕 ● 自分の考えを発表し、（　　）に入る言葉を確認する。 関数 y ＝ a x 2のグラフについて 　�@　関数 y ＝ a x 2のグラフは（放物）線で、その軸は（ y )軸、 　　 頂点は（原点）である。 　�A　関数 y ＝ a x 2のグラフは 　 　a＞０のとき、x軸の上側にあり、（上）に開いている。 　　 a＜０のとき、x軸の下側にあり、（下）に開いている。 深める ○ 教科書77ページの問５を考える。 数学的活動　〔自分の考えを人に伝える活動・人の考えを理解する活動〕 ● グループで答えを確認する。 まとめる 数学的活動　〔自分が行った活動を振り返る活動〕 ● まとめを見ながら、新しい言葉やグラフの特徴を確認する。