|
|
|
単元「式の展開と因数分解」の小単元「因数分解」(5時間)における数学的活動を取り入れた授業展開案です。 |
| |
単元 式の展開と因数分解 (啓林館)
2 因数分解
【・2・ 因数分解】
全5時間
|
| |
| |
ねらい |
・ 因数や因数分解の意味を理解する。 |
| 段階 |
|
| つかむ |
| ○ |
本時の学習内容「多項式を変形してしてみよう」を知る。
|
| ○ |
課題を考える。
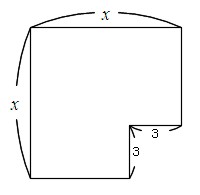
問題『次の図形の面積を求めなさい。』について、
太郎さんは、「私は、正方形から正方形を切り取った図形と考えて、1辺の長さが x の正方形から1辺の長さが3の正方形の面積をひいて、x 2-9 と求めたよ。」と言いました。
花子さんは、「私は、この図形が2つの合同な台形を組み合わせてできた図形と見て、この図形の面積を求めたわ。」と言っています。
花子さんの考えた方法を説明しましょう。
|
|
|
|
| 見通す |
|
| 練り合う |
| ● |
図形から合同な2つの台形をつくり、図形の面積を求める。 |
| 数学的活動 〔自分の考えを人に伝える活動・人の考えを理解する活動〕 |
| ● |
グループのメンバーで互いに、図形の面積の求め方について、自分の考えを説明し合う。 |
| ○ |
図形の面積の求め方を確認する。 |
|
| 深める |
|
| まとめる |
| ● |
授業を振り返り、多項式の因数分解についてノートにまとめる。 |
|
|
|
|
ねらい |
・ 共通因数を取り出して因数分解することができる。
・ 乗法の公式を利用して因数分解することができる。 |
| 段階 |
|
| つかむ |
| ○ |
前時の復習をする。 |
| ○ |
本時の学習内容「多項式の因数分解について学ぼう」を知る。 |
| ○ |
課題を考える。
太郎さんは、M x+M yをM x+M y =M ( x +y ) と因数分解しました。太郎さんの考えについて説明しましょう。
|
|
|
|
| 見通す |
|
| 練り合う |
| ● |
教科書21ページの例1を考える。 |
| ○ |
教科書21ページの問1を考える。 |
| 数学的活動 〔自分の考えを人に伝える活動・人の考えを理解する活動〕 |
| ● |
教科書21ページの問1の考え方について発表する。 |
| ○ |
乗法の公式(和と差の積の公式)を振り返り、a 2 -b 2 =( a +b )( a -b )になることを確認する。 |
|
| 深める |
| ● |
教科書21ページの例2を考える。 |
| ○ |
教科書21ページの問2を考える。 |
|
| まとめる |
| ● |
共通因数を取り出す因数分解の方法や和と差の積の公式を使った因数分解の方法についてまとめる。 |
|
|
|
|
ねらい |
・ 乗法の公式を利用して因数分解することができる。 |
| 段階 |
|
| つかむ |
| ○ |
本時の学習内容「多項式の因数分解について学ぼう」を知る。
|
| ○ |
課題を考える。
問題『x 2 +8 x +16を因数分解しなさい。』について、太郎さんは
x 2 +8 x +16=( x +4) 2 と答えました。
この因数分解が正しいか説明しなさい。 |
|
|
|
| 見通す |
|
| 練り合う |
| 数学的活動 〔自分の考えを人に伝える活動・人の考えを理解する活動〕 |
| ● |
グループのメンバーで互いに、課題についての自分の考えを説明し合う。
|
| ○ |
教科書22ページの例3の説明を聞き、理解する。 |
| ○ |
平方の公式を使った因数分解についてまとめる。
|
| ○ |
教科書22ページの問3を考える。
|
|
| 深める |
| ○ |
教科書22ページの例4の因数分解の説明を聞き、理解する。 |
| 数学的活動 〔自分の考えを人に伝える活動・人の考えを理解する活動〕 |
| ● |
グループのメンバーで互いに、自分の考えを説明し合う。 |
|
| まとめる |
|
|
|
|
ねらい |
・ 乗法の公式を利用して因数分解することができる。 |
| 段階 |
|
| つかむ |
| ○ |
前時の復習をする。 |
| ○ |
本時の学習内容「多項式の因数分解について学ぼう」を知る。 |
|
|
| 見通す |
| ● |
教科書23ページの例5で、x 2 +5 x +6 の因数分解を予想する。 |
|
| 練り合う |
| 数学的活動 〔自分の考えを人に伝える活動・人の考えを理解する活動〕 |
| ● |
因数分解の考え方について発表する。
|
| ○ |
x 2 +5 x +6 の因数分解について確認する。 |
| ○ |
乗法の公式を使った因数分解を確認する。
|
| ○ |
教科書23ページの問6を考える。 |
| ○ |
教科書23ページの例6・例7を考える。 |
| 数学的活動 〔自分の考えを人に伝える活動・人の考えを理解する活動〕 |
| ● |
グループのメンバーで互いに、因数分解の方法について、自分の考えを説明し合う。 |
| ○ |
教科書23ページの問7、教科書24ページの問8を考える。 |
|
| 深める |
|
| まとめる |
| ● |
グループで答えを確認し、因数分解についてまとめる。 |
|
|
|
|
ねらい |
・ 複雑な多項式を因数分解することができる。 |
| 段階 |
|
| つかむ |
| ○ |
前時の復習をする。
|
| ○ |
本時の学習内容「多項式の因数分解について学ぼう」を知る。 |
| ○ |
課題を考える。
a x 2 +6 a x -16 a の因数分解は a ( x -2 )( x +8 ) となります。
どのように考えて因数分解すればよいでしょうか。 |
|
|
|
| 見通す |
|
| 練り合う |
| 数学的活動 〔自分の考えを人に伝える活動・人の考えを理解する活動〕 |
| ● |
計算方法について自分の考えを発表する。 |
| ○ |
発表した意見を基に、因数分解の手順を確認する。 |
| 数学的活動 〔自分の考えを人に伝える活動・人の考えを理解する活動〕 |
|
| 深める |
|
| まとめる |
| ● |
グループで答えを確認し、因数分解についてまとめる。 |
|
|
|
| |
|
| Copyright(C) 2010 SAGA Prefectural Education Center. All Rights Reserved. |
|