|
|
2 研究の実際 |
(3)平成23年度 佐賀県小・中学校学習状況調査の問題分析と指導の手立て
|
平成23年4月に実施しました佐賀県小・中学校学習状況調査の中で、これからの中学校数学科において求められている力やこれまでの調査において本県生徒に課題が見られた力を問うている調査問題を取り上げ、分析をしています。出題の趣旨や調査問題の具体的な内容、調査問題で求められている力やそれらの力を育むための指導について示していますので、これからの指導の参考にしてください。 |
|
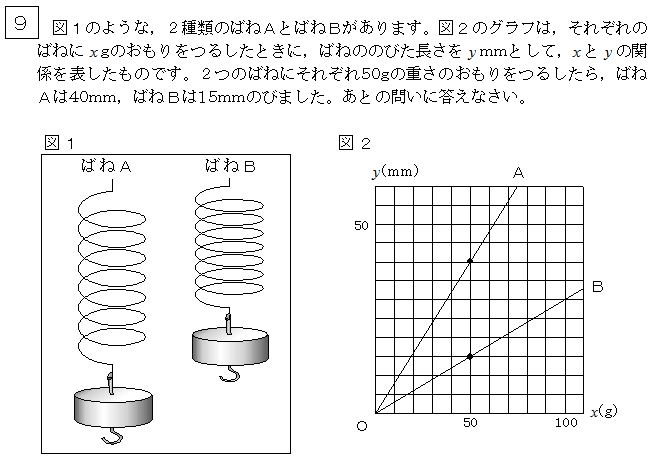
中学2年生 大問9(3) |
学習指導要領に
おける
領域・内容 |
C 関数(第1学年) |
| オ 比例,反比例を用いて具体的な事象をとらえ説明すること |
 |
出題の趣旨 |
| ■ |
事象の変化を読み取り、グラフや式をもとに、数学的に処理することができるかどうかをみます。 |
|
問題の内容 |
| ■ |
与えられたグラフ、またはグラフから導き出される関係式をもとに、答え(おもりの個数)を導き、答えを導く過程をことばや式を使って説明する問題です。 |
|
この問題で求められている力 |
| この問題では、次の3つの力が求められています。 |
| ■ |
与えられたグラフからおもりの重さ( x g)とばねの長さ( y mm)の関係を読み取る力 |
| ■ |
与えられた y の値(20mm)に対応する x の値をとらえて答えを導く力 |
| ■ |
さらに答えを導く過程をことばや式を使って数学的に説明する力 |
|
| 求められている力を育むための指導例 |
| ■ |
まずは、グラフから( x ,y )の値の組を読み取ることや、x の値から y の値を導くだけでなく、y の値から x の値を導くことの指導を行う必要があります。 |
| ■ |
グラフや式から値を求めるだけでなく、この問題のように x の値が整数値の間となった場合に、条件を満たすものを自分で判断し、選択していく場面も取り入れていく必要があります。 |
| ■ |
グラフから式を求める際、x 軸と y 軸の1目もりが表す数値の大きさが違う場合において、x と y の関係をとらえきれない生徒が多く見られますので、関数の利用の場面で、そのような問題にできるだけ触れさせる事が大切です。 |
| ■ |
この問題では、グラフと式のどちらかを選択して説明することとなっていますが、グラフからの考え方だけでなく、グラフから式を導き、それを基に値を求めて、答えを条件に合うように判断するという両方の考え方ができるように指導していく必要があります。 |
|
|
| Copyright(C) 2010 SAGA Prefectural Education Center. All Rights Reserved. |
|