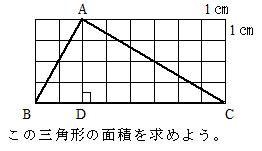
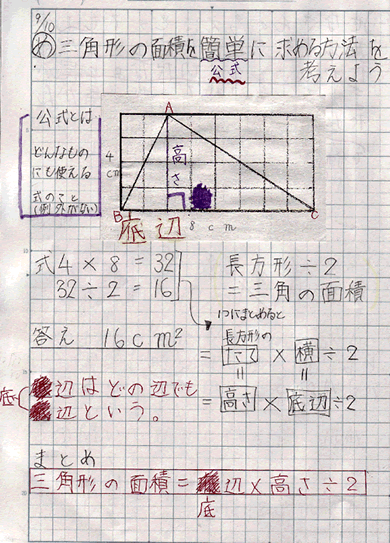
| 小学5年 「面積の求め方を考えよう」 3/12時の学習プラン ~三角形の面積を簡単に求める方法を考えよう~ |
| 1 本時の目標 | |||||||||||||||||||||||||||||||||||
○ |
三角形の面積を求める公式を考えることができる。【表現・処理】 | ||||||||||||||||||||||||||||||||||
| 2 主な算数的活動について | |||||||||||||||||||||||||||||||||||
○ |
探究的な活動として、三角形の面積が長方形の面積の半分の大きさであることから式化する。その際、長方形の縦と横が三角形のどの部分の長さと同じであるのかを図に線を書き込みながら具体的にとらえさせる。また、三角形の「底辺」と「高さ」を固定したものと考えないように図形を回転させる操作により、どこを底辺として考えるかによって高さが決まることをはっきりとつかませる。 | ||||||||||||||||||||||||||||||||||
○ |
説明する活動として、長方形の場合の縦と横の長さをどのように考えたかを明らかにして説明させる。 | ||||||||||||||||||||||||||||||||||
| 3 | 本時の展開 | ||||||||||||||||||||||||||||||||||
※ 前時の学習内容を振り返り、長方形の縦や横の長さに当たる部分を意識させます。 |
|||||||||||||||||||||||||||||||||||
| Copyright(C) 2009 SAGA Prefectural Education Center. All Rights Reserved. |
| 最終更新日:. 2010-06-28 |