| 小学5年 「面積の求め方を考えよう」 10/12時の学習プラン 〜高さや底辺によって三角形の面積がどのように変化するか調べよう〜 |
| 1 本時の目標 | ||||||||||||||||||||||||||||||||||||||
○ |
三角形の面積を求める公式で、高さや底辺を変えたときの面積との関係を調べることができる。【数学的な考え方】 | |||||||||||||||||||||||||||||||||||||
| 2 主な算数的活動について | ||||||||||||||||||||||||||||||||||||||
○ |
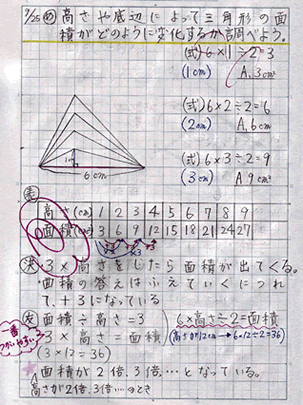
作業的な活動として、底辺が同じで高さが変化する三角形を考え、その面積の変化を計算によって求めさせる。その際、数値だけでなく、具体的な図を用いて面積の変化をとらえさせる。 | |||||||||||||||||||||||||||||||||||||
○ |
探究的な活動として、三角形の高さと面積の変化を表にまとめながら、伴って変わる2量の変化の様子を調べさせる。この学習を通して、関数的な見方・考え方の素地を養う。 | |||||||||||||||||||||||||||||||||||||
○ |
説明する活動として、三角形の高さと面積の変わり方を調べて、分かったことを自分なりの言葉で説明させる。 | |||||||||||||||||||||||||||||||||||||
| 3 本時の展開 | ||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||
| Copyright(C) 2009 SAGA Prefectural Education Center. All Rights Reserved. |
| 最終更新日: 2010-06-28 |