y軸周りの回転体の体積を求めるには、通常、教科書に掲載されている次の公式
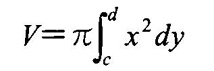 |
を利用しますが、大学入試の場合、回転させる関数y=f(x)は凹凸のある形状であることが多く、場合分けが必要で、
計算が煩雑になる問題がほとんどです。そこで場合分けが少なく、一度の計算で体積を求めるのに有力な、バーム
クーヘン積分と呼ばれている方法を紹介します。
【バームクーヘン積分の考え方】
y軸の周りの回転体の体積を考える場合、y軸に垂直な断面(=円)の面積をy=cからy=dまでの定積分として求め
ますが、バームクーヘン積分の考え方は、回転体の体積を円の中心がy軸上にある円柱の側面積のx=aからx=b
までの定積分として考える方法です。(次図)
| 関数y=f(x)のx=aからX=bまでの部分をy軸の周りに回転する |
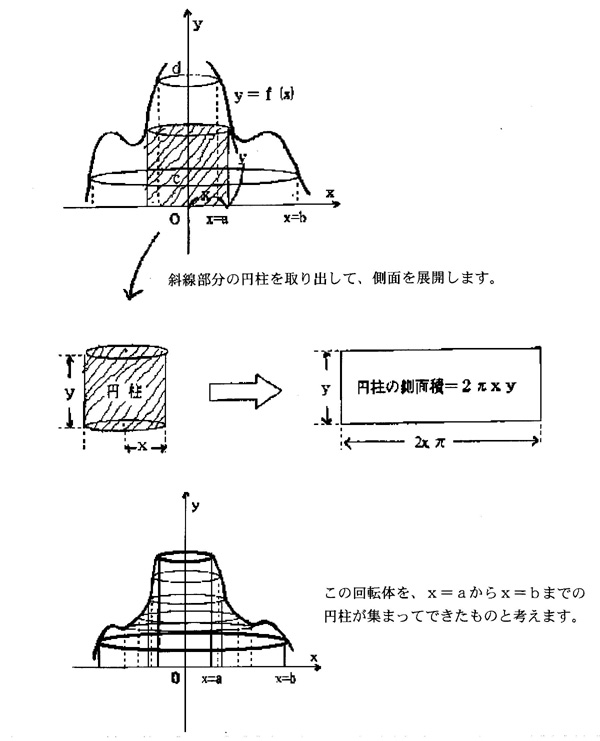 |
| 半径がaのときからbのときまでの円柱の側面積を連続的に加えていくと、回転体の体積が求まります。 円柱が幾重にも重なっている様子が洋菓子のバームクーヘンに似ていることからバームクーヘン積分の名があります。 バームクーヘン積分は、x軸やy軸の周りの回転体の体積を求める場合に有力な方法です。 |
求める回転体の体積は次の計算で求めることができます。
(ただし、計算するには変数yを変数xで表す必要があります。)
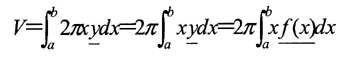 |
出題例: H16 同志社大
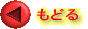 |